Course Homepage for Advanced Computational Statistics (PhD Course 2023; 7.5 HEC)
SummaryStatistics depends heavily on computational methods. Optimisation methods are used in statistics for example for maximum likelihood estimates, optimal experimental designs, risk minimization in decision theoretic models. In these cases, solutions of optimisation problems usually do not have a closed form but need to be computed numerically with an algorithm. Another big demand on computational methods is when statistical distributions are simulated and integrated and statistics of these distributions have to be determined in an efficient way.
This course focuses on computational methods for optimisation, simulation and integration needed in statistics. The optimisation part discusses gradient based, stochastic gradient based, and gradient free methods. Further, constrained optimisation will be a course topic. We will discuss techniques to simulate efficiently for solving statistical problems.
We will use implementation with the programming language R. Examples from machine learning and optimal design will illustrate the methods.
Most welcome to the course!
Frank Miller, Department of Computer and Information Science, Linköping University
frank.miller at liu.se
Lectures: March 16; Time 13-17. Linköping University, Campus Valla. Room: KG44, Building Key (floor 4; building is next to studenthuset).
Reading:
- Givens GH, Hoeting JA (2013). Computational Statistics, 2nd edition. John Wiley & Sons, Inc., Hoboken, New Jersey. Chapter 2 until 2.2.3 (and Chaper 1.1-1.4 if needed).
- Goodfellow I, Bengio Y, Courville A (2016). Deep Learning. MIT Press, http://www.deeplearningbook.org. Chapter 4.3 (and parts of Chapter 2 and Chapter 4.2 if needed).
- Sun S, Cao Z, Zhu H, Zhao J (2019). A survey of optimization methods from a machine learning perspective, https://arxiv.org/pdf/1906.06821.pdf. Section I, II, IIIA1, IIIB1-2.
- AlphaOpt (2017). Introduction To Optimization: Gradient Based Algorithms, Youtube video (very elementary introduction of concepts).
- About analytical optimisation. (Frank Miller, March 2023)
- Understanding gradient descent. (Eli Bendersky, August 2016)
- Bisection method. (Frank Miller, March 2020; 4min video)
Example code: steepestascentL1.r
 Topic 2: Stochastic gradient based optimisation
Topic 2: Stochastic gradient based optimisation
Lectures: March 17; Time 9-12. Linköping University, Campus Valla. Room: John von Neumann, B Building (floor 3, entrance 27).
Reading:
- Goodfellow I, Bengio Y, Courville A (2016). Deep Learning. MIT Press, http://www.deeplearningbook.org. Chapter 5.9 and 8.1 to 8.6 (and other parts of Chapter 5 based on interest).
- Sun S, Cao Z, Zhu H, Zhao J (2019). A survey of optimization methods from a machine learning perspective, https://arxiv.org/pdf/1906.06821.pdf. Section IIIA2-6, IIIB3 (other sections upon interest).
- Ruder S (2016). An overview of gradient descent optimization algorithms. https://arxiv.org/pdf/1609.04747.pdf
- Goh G (2017). Why momentum really works. Distill. https://distill.pub/2017/momentum/ (includes a derivation of the optimal step size in steepest ascent, and optimal parameters for momentum method).
- Mitliagkas I (2018/2019). IFT 6085 - Lecture 5; Accelerated Methods - Polyak's Momentum (Heavy Ball Method). http://mitliagkas.github.io/ift6085-2019/ift-6085-lecture-5-notes.pdf (includes a simplified derivation of the optimal step size in steepest ascent, and optimal parameters in Polyak's momentum).
- Mitliagkas I (2018/2019). IFT 6085 - Lecture 6; Nesterov's Momentum, Stochastic Gradient Descent. http://mitliagkas.github.io/ift6085-2019/ift-6085-lecture-6-notes.pdf (Example for non-convergence of Polyak's momentum method and description of Nesterov's momentum method).
Dataset: logist.txt
Assignment for Lecture 1 and 2
Topic 3: Gradient free optimisationLectures: April 4; Time 10-12 and 13-15. Online via Zoom (link will be sent to registered participants by email).
Reading:
- Givens GH, Hoeting JA (2013). Computational Statistics, 2nd edition. John Wiley & Sons, Inc., Hoboken, New Jersey. Chapter 3.1 to 3.3 (and 2.2.4).
- AlphaOpt (2017). Introduction To Optimization: Gradient Free Algorithms (1/2) - Genetic - Particle Swarm, Youtube video (elementary introduction of concepts).
- AlphaOpt (2017). Introduction To Optimization: Gradient Free Algorithms (2/2) Simulated Annealing, Nelder-Mead, Youtube video (elementary introduction of concepts).
- Clerc M (2012). Standard Particle Swarm Optimisation. 15 pages. https://hal.archives-ouvertes.fr/hal-00764996 (some background to details in implementation including choice of parameter values).
- Wang D, Tan D, Liu L (2018). Particle swarm optimization algorithm: an overview. Soft Comput 22:387-408. (Broad overview over research about PSO since invention).
- Bonyadi MR, Michalewicz Z (2016). Stability analysis of the particle swarm optimization without stagnation assumption. IEEE transactions on evolutionary computation, 20(5):814-819.
- Cleghorn CW, Engelbrecht AP (2018). Particle swarm stability: a theoretical extension using the non-stagnate distribution assumption. Swarm Intelligence, 12(1):1-22. An author version is available here.
- Clerc M (2016). Chapter 8: Particle Swarms. In: Metaheuristics. (Siarry P ed.).
- Goodfellow I, Bengio Y, Courville A (2016). Deep Learning. MIT Press, http://www.deeplearningbook.org. Chapter 5.2 and 7.1 (not about gradient free but about regularisation as background for Problem 3.2).
Example code: PSO_order1_stability.r
Code for Problem 3.4: crit_HA3.r
Dataset for Problem 3.2, 4.2, and 5.2: cressdata.txt.
 Topic 4: Optimisation with constraints
Topic 4: Optimisation with constraints
Lecture: April 18, Time 10-12 and 13-15. Online via Zoom (same link as for Lecture 3).
Reading:
- Goodfellow I, Bengio Y, Courville A (2016). Deep Learning. MIT Press, http://www.deeplearningbook.org. Chapter 4.4-4.5 and 7.2.
- Lange K (2010). Numerical Analysis for Statisticians. Springer, New York. Chapter 11.3-11.4 (Optimisation with equality and inequality constraints) and Chapter 16.1-16.3 and 16.5 (Barrier method, model selection and the lasso).
Program for D-optimal design for quadratic regression in Lecture 4 using constrOptim: L4_Doptdesign_constrOptim.r. Code from lecture slides for Problem 4.3: L4_Code_for_problem4-3.r.
 Topic 5: EM algorithm and bootstrap
Topic 5: EM algorithm and bootstrap
Lecture: May 2, Time 10-13. Online via Zoom (same link as for Lecture 3).
Reading:
- Givens GH, Hoeting JA (2013). Computational Statistics, 2nd edition. John Wiley & Sons, Inc., Hoboken, New Jersey. Chapter 4.1-4.2.2 and 9.1-9.3, 9.7.
- Lindholm A, Wahlström N, Lindsten F, Schön TB (2022). Machine Learning - A First Course for Engineers and Scientists. Cambridge University Press, http://smlbook.org/book/sml-book-draft-latest.pdf. Chapter 10.1-10.2, 7.1.
- Bishop CM (2006). Pattern Recognition and Machine Learning. Springer, New York. Chapter 9. https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
- Wicklin R (2017). The bias-corrected and accelerated (BCa) bootstrap interval. SAS blogs. https://blogs.sas.com/content/iml/2017/07/12/bootstrap-bca-interval.html
Code for Problem 5.1: emalg.r
Dataset for Problem 5.1: bivardat.csv.
 Topic 6: Simulation of random variables
Topic 6: Simulation of random variables
Lecture: May 16, Time 13-17. Stockholm University, Albano, hus 4, floor 6 (Department of Statistics). Styrelserummet.
Entrance: See Red 0 on this map. Go then to the next stairs/elevator; take the elevator to floor 5 and then the stairs to floor 6 (OBS: You have to knock on the door to come in! Alternative: Go to Zone Q in hus 4, take the elevator to floor 6 and you can open the door to the Stats department)
To come to Albano (link to Google maps: Albanovägen 12):
Tunnelbana (underground) stations "Universitetet" and "Tekniska högskolan" are both in 15-20 minutes walking distance. Closest is the buss stop "Albano" (square B3 on the map). You can take bus 50 from tunnelbana "Universitetet" or from Odenplan to the bus stop "Albano".
Reading:
- Givens GH, Hoeting JA (2013). Computational Statistics, 2nd edition. John Wiley & Sons, Inc., Hoboken, New Jersey. Chapter 6.1-6.3.1, 7.1, and 7.3.
Code for example "Type I error under wrong distribution": typeIerrorSimulation.r
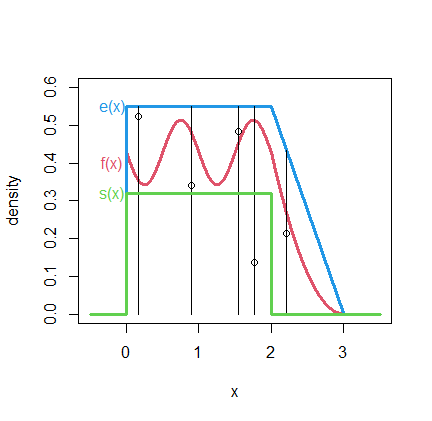 Topic 7: Numerical and Monte Carlo integration; importance sampling
Topic 7: Numerical and Monte Carlo integration; importance sampling
Lecture: May 17, Time 9-12. Stockholm University, Albano, hus 4, floor 6 (Department of Statistics). Styrelserummet.
Reading:
- Givens GH, Hoeting JA (2013). Computational Statistics, 2nd edition. John Wiley & Sons, Inc., Hoboken, New Jersey. Chapter 5.1, 5.3, and 6.4.1-6.4.2.
- Owen AB (2013). Monte Carlo theory, methods and examples. https://artowen.su.domains/mc/Ch-var-is.pdf. Chapter 9.1-9.5.
Assignment for Lecture 6 and 7
 Prerequisites
Prerequisites
Accepted to a doctoral program in Sweden in Statistics or a related field (e.g. Mathematical Statistics, Engineering Science, Quantitative Finance, Computer Science). Knowledge about Statistical Inference (e.g. from the Master's level) and familiarity with a programming language (e.g. with R) is required.
Note that the content of the optimisation part of the course will have considerable overlap with the Ph.D. courses Optimisation algorithms in Statistics I/II which I gave in 2020/2021, i.e. the current course is not intended for the participants of the former courses.
ContentThe course contains fundamental principles of computational statistics. Focus is on:
- Principles of gradient based and gradient free optimisation including stochastic optimisation and constrained optimisation
- Introduction to convergence analysis for stochastic optimisation algorithms
- Statistical problem-solving using optimisation, including maximum likelihood, regularized least squares, and optimal experimental designs
- Principles of numerical integration
- Principles of statistical simulation
- The bootstrap method
- Statistical problem-solving using simulation techniques including generation of Monte Carlo estimates, their confidence intervals, and posterior distributions
On completion of the course, the student is expected to be able to:
- Demonstrate knowledge of principles of computational statistics
- Explain theoretical and empirical methods to compare different algorithms
- Design and organize algorithms for optimisation, integration, and simulation of distributions
- Solve statistical computing problems using advanced algorithms
- Adapt a given optimisation, integration, or simulation method to a specific problem
- Assess, compare and contrast properties of alternative optimisation, integration, and simulation methods
- Critically judge different methods for optimisation, integration, and simulation
- Ability to choose an adequate method for a given statistical problem
The intended learning outcomes will be graded by several individual home assignments. The grades given: Pass or Fail.
Course Literature- Givens GH, Hoeting JA (2013). Computational Statistics, 2nd edition. John Wiley & Sons, Inc., Hoboken, New Jersey.
- Goodfellow I, Bengio Y, Courville A (2016). Deep Learning. MIT Press, http://www.deeplearningbook.org. Focus on Chapter 4, 5, and 8.
- Further literature including research articles and other learning material will be provided in the course.
Lectures and some problem sessions. The teaching is conducted in English. Course participants will spend most of their study time by solving the problem sets for each topic on their own computers without supervision. The course will be held in March, April, and May 2023.
- Lecture 1: Gradient based optimisation
March 16, 13:00-17:00 (in Linköping) - Lecture 2: Stochastic gradient based optimisation
March 17, 9:00-12:00 (in Linköping) - Lecture 3: Gradient free optimisation
April 4, 10:00-12:00, 13:00-15:00 (online, Zoom) - Lecture 4: Optimisation with constraints
April 18, 10:00-12:00, 13:00-15:00 (online, Zoom) - Lecture 5: EM algorithm and bootstrap
May 2, 10:00-13:00 (online, Zoom) - Lecture 6: Simulation of random variables
May 16, 13:00-17:00 (in Stockholm) - Lecture 7: Importance sampling
May 17, 9:00-12:00 (in Stockholm)
To register for the course, please send an email to me (frank.miller at liu.se) until February 20, 2023. You are also welcome for any questions related to the course.